信息论科普：GPT对给定序列无损压缩的最终区间

可以用GPT无损压缩的算术编码作为例示

一、最终区间的本质：概率宇宙中的精确坐标

想象一个包含所有可能文本序列的宇宙（概率空间）：

[0,1) 区间 = 所有可能文本序列的总集合

• • 每个特定序列（如"人工智能将改变世界"）对应宇宙中的一个专属子区间

  • 子区间长度 = 该序列出现的概率（由语言模型GPT计算得出）

  • 子区间位置 = 该序列在概率空间中的唯一坐标

二、区间长度=概率的数学证明

假设序列由3个词组成：

序列：W1 → W2 → W3
概率：P(W1) = 0.4, P(W2|W1) = 0.6, P(W3|W1,W2) = 0.8

区间变化过程：

初始： [0, 1)        长度=1.0
选W1： [0, 0.4)      长度=0.4  (1.0×0.4)
选W2： [0.16, 0.4)   长度=0.24 (0.4×0.6)
选W3： [0.16, 0.352) 长度=0.192(0.24×0.8) ← 最终区间长度=0.192

最终长度 = P(W1)×P(W2|W1)×P(W3|W1,W2) = 序列概率

三、宇宙坐标系统的运作原理

示例：压缩序列 ["猫", "吃", "鱼"]

编码/压缩过程：

1. 1. 编码"猫"：

      [0, 1) → 划分：
        猫：[0, 0.5)
        狗：[0.5, 0.8)
        鱼：[0.8, 1)
      选择 [0, 0.5)

   2. 编码"吃" (上下文="猫")：

      当前区间 [0, 0.5)
      语言模型新分布：P(吃|猫)=0.7, P(睡|猫)=0.3
      划分：
        吃：[0, 0.5×0.7)= [0, 0.35)
        睡：[0.35, 0.5)
      选择 [0, 0.35)

   3. 编码"鱼" (上下文="猫吃")：

      当前区间 [0, 0.35)
      语言模型新分布：P(鱼|猫吃)=0.4, P(肉|猫吃)=0.6
      划分：
        鱼：[0, 0.35×0.4)= [0, 0.14)
        肉：[0.14, 0.35)
      选择 [0, 0.14)

最终结果：

序列 ["猫","吃","鱼"] → 独占宇宙坐标 [0, 0.14)
区间长度 = 0.14 = 0.5×0.7×0.4

四、为什么这是唯一坐标？数学保证

假设存在两个不同序列A和B，它们对应的最终区间重叠：

A区间: [L_A, R_A)
B区间: [L_B, R_B)
且 [L_A, R_A) ∩ [L_B, R_B) ≠ ∅

根据算术编码原理：每个序列的区间由其唯一词路径决定

若A和B在第k个词首次不同：

• • 第k步时，A和B会选择不相交的子区间

  • 后续划分永远在分离的区间进行
    → 矛盾！ 故不同序列的区间互不相交

五、解码/解压：从坐标回溯序列

给定最终区间 [0, 0.14) 和相同语言模型GPT：

当前区间 [0,1)
数值 C=0.09（区间内任意点）

步骤1：划分初始区间
   [0,0.5) → 猫
   [0.5,0.8) → 狗
   [0.8,1) → 鱼
   C=0.09 ∈ [0,0.5) → 输出"猫"

步骤2：缩放区间
   新区间 = [0,0.5)
   缩放C = (0.09-0)/(0.5-0) = 0.18
   划分：
       吃：[0,0.35) → [0,0.35)相对值→ [0,0.7)
       睡：[0.35,0.5) → [0.7,1)
   C=0.18 ∈ [0,0.7) → 输出"吃"

步骤3：再次缩放
   新区间 = [0,0.35)
   缩放C = (0.18-0)/(0.7-0)×0.35 = 0.09
   划分：
       鱼：[0,0.14) → [0,0.4)
       肉：[0.14,0.35) → [0.4,1)
   C=0.09 ∈ [0,0.4) → 输出"鱼"

完美还原序列！

六、宇宙坐标的直观展示

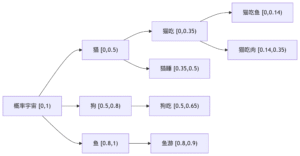
每个叶节点是最终区间；节点深度越深，区间越小；路径唯一性：从根到叶的每条路径对应唯一序列。

七、工程意义：为何这是革命性的

1. 突破分组限制：

   • 传统压缩（如Huffman）需将符号分组处理

   • 算术编码实现连续流式压缩，单个比特代表部分信息

2. 逼近熵极限：

   理论最小体积 = -log₂(P(序列)) 比特
   算术编码体积 ≈ ceil(-log₂(P(序列)))

   例如P=0.14 → -log₂(0.14)≈2.84 → 3比特足够

3. 大模型赋能：

   • GPT类模型提供精准的 P(word|context)

   • 对自然语言序列，P(序列)值大幅提高 → 区间长度更大 → 所需比特更少

最终区间是概率宇宙中的神圣坐标，它用数学的纯粹性证明：信息即概率，概率即几何，而完美的无损压缩，不过是在[0,1)区间为每条路径划定它应得的疆域。

• 立委关于大模型与AI的博客汇总